一切的起源-Tweedie公式
分数函数可以用于去除噪声
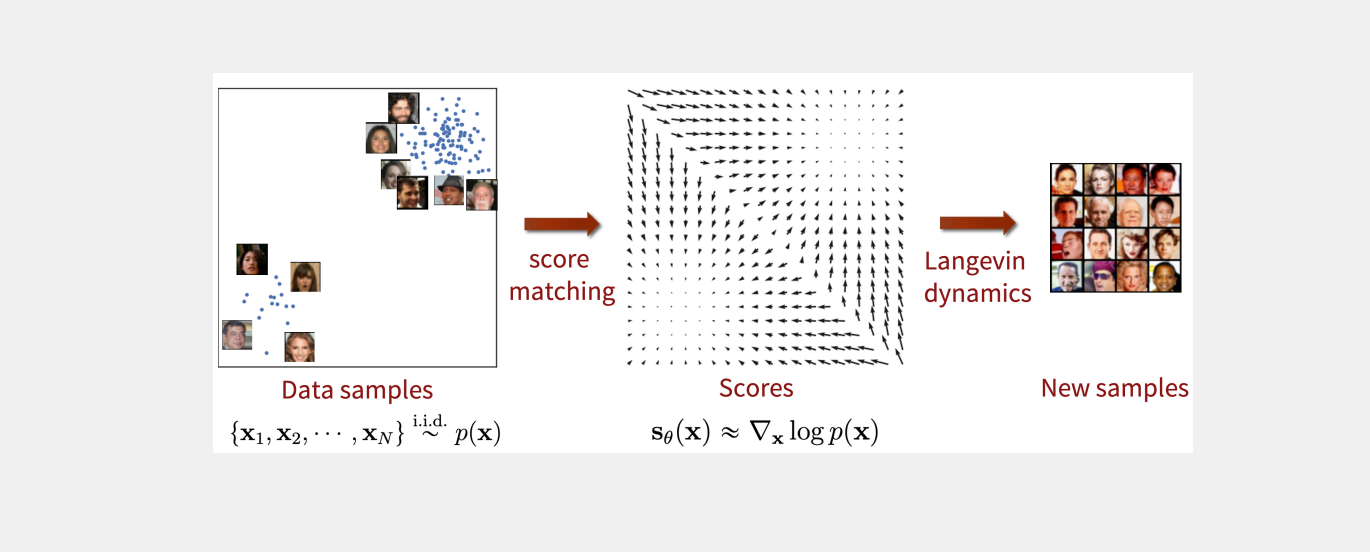
SGM的一个核心特定就是它将训练过程和采样过程解耦，其与DDPM有本质的不同，就是其模型专注于学习数据分布的梯度（分数函数）来实现的，而不是直接生成数据，一旦训练完成，分数函数就可以独立于训练数据用于采样。
有学者已经证明，使用分数函数有多种采样方法，通常使用Langevin动力学或其他类型的马尔可夫链蒙特卡罗（MCMC）方法。
退火Langevin动力学
核心公式：
可以证明，当α→0且T→∞时，xT可以无限趋近于真实样本
使用去噪分数匹配进行训练：
但Langevin动力学存在以下问题：
- 只有当加入噪声很小时，去噪分数匹配的分数估计才能符合，同时在数据密度较低的区域，分数估计又非常不准确，这导致Langevin采样更不准确了
- 当加入噪声很大时，分数估计表现良好，但得到的数据分布仍保留部分加入的噪声，真实数据分布被破坏
解决方法：采用退火的思想，在采样时先加大噪声后加小噪声对数据进行扰动，用同一分数网络预测不同噪声下数据的分数函数(这里思想和DDPM出奇相似)，再采用Langevin动力学。在接近目标数据分布后，再次施加较小的噪声，并使用更小的步长进行更多的Langevin动力学迭代。这有助于细化样本，调整细节，使其更精确地匹配真实数据分布。
按以上原理，训练的网络需要在各种噪声条件下准确预测对应的分数函数，则输入需要包含噪声大小，可以用以下方法训练(称为NCSN网络)，通过实验，使用U-Net、空洞卷积和transformer的网络效果最好
算法：退火Langevin动力学
数列最好设置为等比数列，参数更新时加上EMA更稳定